Introduction¶
This section is going to be much shorter than the last one. We don’t want to go deep into models that are more biophysically realistic, but we do want to mention them.
Hodgkin-Huxley type neuron¶
We’ll start with the famous Hodgkin-Huxley neuron. You can see an action potential plotted with this model here.
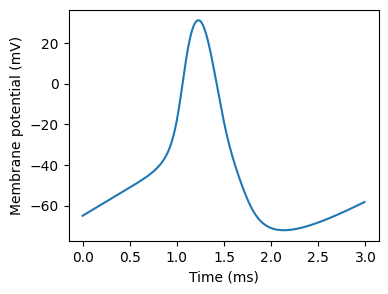
Figure 1:Action potential in a Hodgkin-Huxley model.
These models are derived by treating the cell membrane as an electrical circuit consisting of a capacitor and a number of voltage-dependent resistors corresponding to the different ion channels. Each type of ion channel has an associated current with its own dynamics, and there are many different types.
Actually, there are thousands of papers on different types of ion channels and their associated dynamics. In the original paper Hodgkin & Huxley, 1952 they considered just three channels corresponding to sodium (Na), potassium (K) and a leak (L).
By hand - quite literally as they used a hand cranked mechanical calculator to solve the equations over several weeks - they found a series of functions that approximated these dynamics quite well.
Their model fitted , and into equations like this.
With the functions defined like so:
Ultimately, this comes down to a nonlinear differential equation with four dynamic variables and a lot of choices of functions and constants to fit to data.
It’s also a bit of a nasty one to simulate, either requiring very small time steps or a specific numerical integration method.
For more
This has just been a very quick glimpse at this type of model. We’ve provided an example of the code to simulate these in 💻 Code for figures.
Further reading:
Spatial / Multicompartamental Neuron¶
One thing we’ve totally ignored so far in all the models we’ve talked about is that neurons have a very complex spatial structure, with dendrites and axons and - as you can see in the picture - activity that travels around the cell.
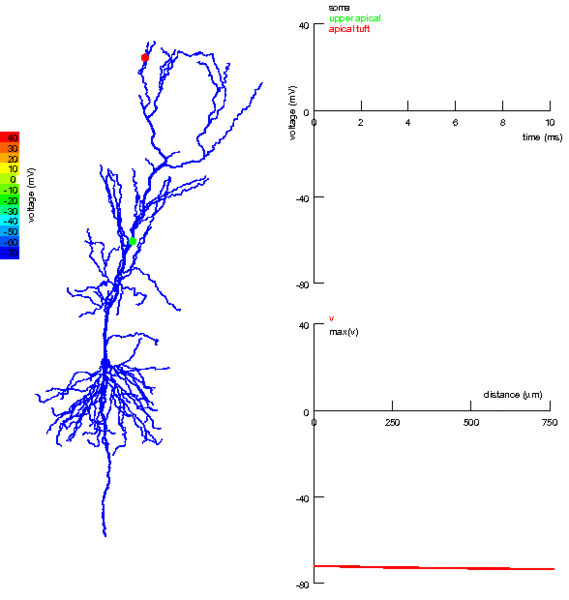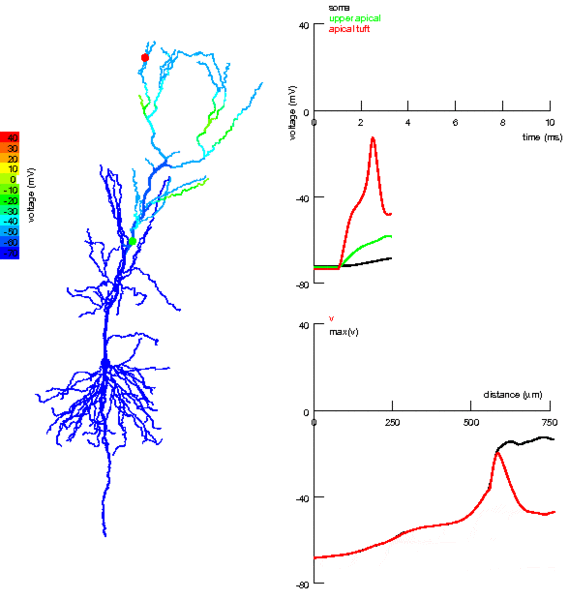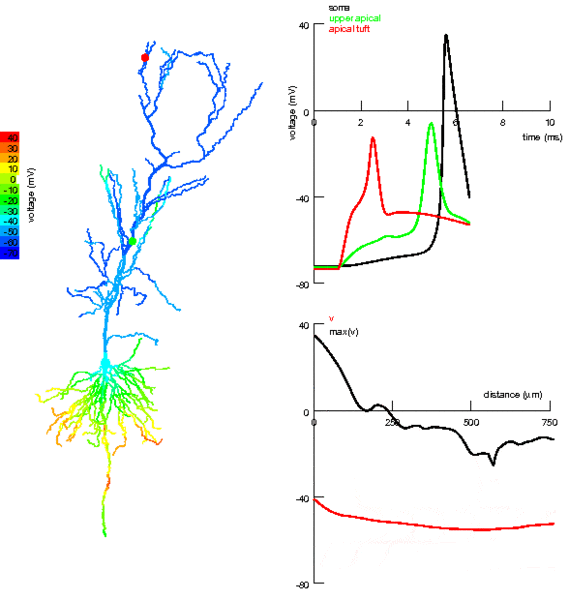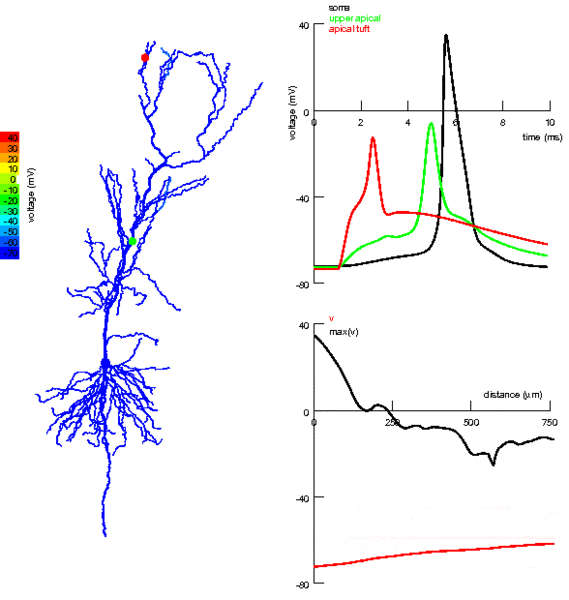
Figure 3:Propagation of electrical activity in a multicompartmental neuron model.
We can capture this by thinking of the dendrites and axons as cylinder, then break these cylinders into a number of short cylindrical segments that are relatively uniform. We then think of each as being nodes in an electrical circuit as we did with the Hodgkin-Huxley neuron.
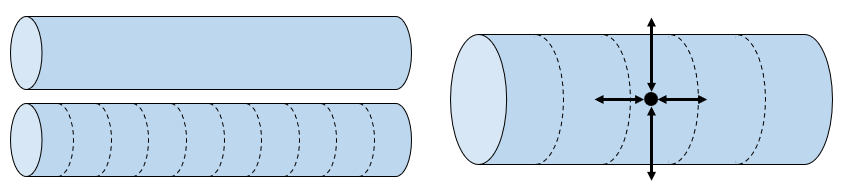
Figure 4:Modelling dendrites and axons as cylinders broken into compartments.
If we take this approach and follow the mathematical analysis through, we get the cable equation, a second order partial differential equation. This can be simulated by breaking the cable into compartments as above, but as you can imagine it gets quite heavy quite quickly, as real neurons can have thousands of these compartments that need to be simulated.
So, does any of this matter in terms of how the network as a whole functions or is this just implementation details?
We don’t know, but it has been argued that it may be important and it’s an active area of research, for example see Pagkalos et al. (2023).
The problem is that it’s too computationally demanding to be used in a machine learning setup, or indeed in a large network without huge computational resources.
Dendrify¶
That’s where Dendrify comes in. It’s a relatively new software package to automatically simplify these very complex models into something that can be easily simulated while still capturing a lot of the relevant dynamics, like these examples here. If you’re interested in exploring what dendritic structure could add to network level computations, this package is probably worth a look.
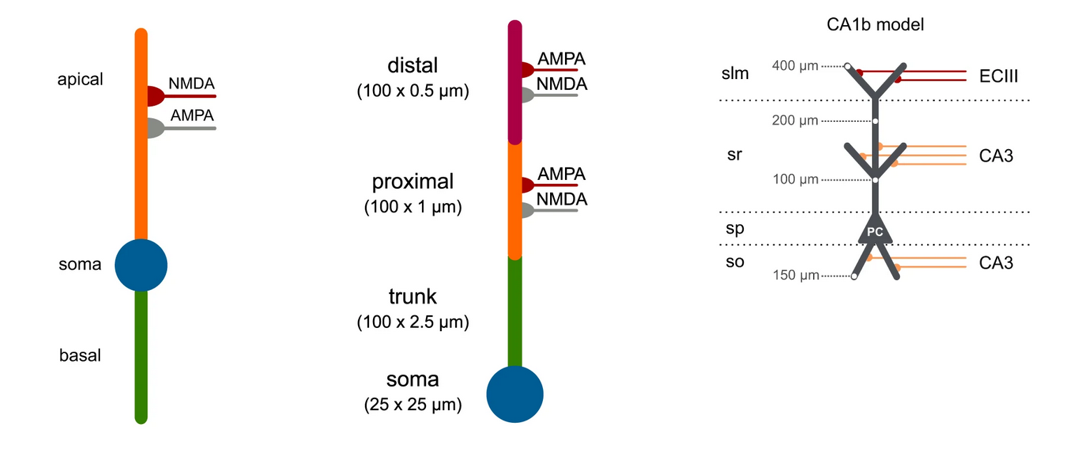
Figure 5:Simplified multicompartmental neurons as used in Dendrify.
- Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117(4), 500–544. 10.1113/jphysiol.1952.sp004764
- Pagkalos, M., Makarov, R., & Poirazi, P. (2023). Leveraging dendritic properties to advance machine learning and neuro-inspired computing. arXiv. 10.48550/ARXIV.2306.08007